You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Do same rules of Brilliant apply to Princess?
- Thread starter 1st_time
- Start date
- Status
- Not open for further replies. Please create a new topic or request for this thread to be opened.
No. A Princess is a fancy cut with different crown/pavillion and multiple combinations.
There are some old cut-charts with the basic proportions that a Princess should have but there is too much interplay between the different facets and angles to go by numbers alone. Hence, if you want to play it super-safe to know you have an ideal Princess - you need an ASET (or at the very least an IS) or preferably - one that has been graded by the AGS as 000 ideal.
A princess should have a medium or slightly thick girdle as the corners are more prone to chipping.
There are some old cut-charts with the basic proportions that a Princess should have but there is too much interplay between the different facets and angles to go by numbers alone. Hence, if you want to play it super-safe to know you have an ideal Princess - you need an ASET (or at the very least an IS) or preferably - one that has been graded by the AGS as 000 ideal.
A princess should have a medium or slightly thick girdle as the corners are more prone to chipping.
Maisie
Super_Ideal_Rock
- Joined
- Dec 30, 2006
- Messages
- 12,598
- Joined
- Apr 30, 2005
- Messages
- 42,064
Welcome

Yes, Princess cuts are a different kettle of fish when judging the all important cut, but I would say to hold off a bit if you can and learn a bit more about the shape before buying, that is a lot of money and you want to get it right. Really see what your options are for your lovely budget before taking the plunge, it is easy to rush in and regret your purchase.
 You could make things much easier by consulting a reputable online vendor such as Whiteflash, Good old Gold, James Allen, Wink Jones - they are experts and won't steer you wrong.
You could make things much easier by consulting a reputable online vendor such as Whiteflash, Good old Gold, James Allen, Wink Jones - they are experts and won't steer you wrong.

Yes, Princess cuts are a different kettle of fish when judging the all important cut, but I would say to hold off a bit if you can and learn a bit more about the shape before buying, that is a lot of money and you want to get it right. Really see what your options are for your lovely budget before taking the plunge, it is easy to rush in and regret your purchase.

- Joined
- Apr 30, 2005
- Messages
- 42,064
There are some good vendors in the DD apparently, but it is said you need to be very cautious - have you looked online to see what is available for the budget??? It is also best to use a vendor who has a good return policy and will let you have the diamond appraised by an independant expert, this is a good safeguard.
Maisie
Super_Ideal_Rock
- Joined
- Dec 30, 2006
- Messages
- 12,598
JohnQuixote
Ideal_Rock
- Joined
- Sep 9, 2004
- Messages
- 5,212
Don''t exclude a thin girdle out of hand: This is where the skill of the setter is as important (more in fact) as the cut of the diamond. Thin, medium and stk are all acceptable girdle averages and a setter worth his salt can set them equally well. In fact, if a girdle average is medium and the range runs from very thin to medium there may be nothing to worry about: Corners are naturally vulnerable on princess cuts, but the ''very thin'' as a range indicator only may imply a single extremely small spot (or perhaps an indented natural) which is nowhere near the vulnerable corners and no cause for worry. Determining vulnerability must be done on a case-by-vase basis.Date: 1/17/2007 10:26:48 AM
Author: tanalasta
No. A Princess is a fancy cut with different crown/pavillion and multiple combinations.
There are some old cut-charts with the basic proportions that a Princess should have but there is too much interplay between the different facets and angles to go by numbers alone. Hence, if you want to play it super-safe to know you have an ideal Princess - you need an ASET (or at the very least an IS) or preferably - one that has been graded by the AGS as 000 ideal.
A princess should have a medium or slightly thick girdle as the corners are more prone to chipping.
When it comes to tension settings, where entire sides of the girdle take pressure, staying with medium and above is certainly advisable.
- Joined
- Sep 2, 2002
- Messages
- 2,859
My reply might surprise you, but I think that princess-cuts follow the same rules as rounds. After all, it is the same material, diamond, and it is the same light entering from the environment, isn''t it?
The problem lies in notation and in perception, though. I will keep my maths as simple as possible.
Let us look at the pavilion of a round. We agree that we should have good symmetry and a pavilion-angle of around 41°, thus resulting in a pavilion depth of around 43%.
In a princess-cut, the P2-angle, going from the point to the culet, should also be around 41°. But because the depth of a princess is not a factor of the average diameter (like in rounds), but of the smallest diameter, this changes the depth-percentage. Since the facet goes from the corner to the culet, the depth is about 43% of the longest diameter (from point to point). In gemology however, we use the smallest diameter as a reference, and suddenly, the same pavilion-angle causes a depth of slightly over 60%. So, same rules, same angle, but different notation.
In the same way, I like a crown angle in a princess-cut, which is around 34°. Reminds me a lot of what I like in a round.
They have become different animals, however, because the notation of the proportions is different. If you have a princess with a total depth of 63%, this would be under 55%, if we would calculate it in the same way as in a round. Are you sure that you would want to have a round with only 53%-depth?
Sorry, I am beginning to ramble. I hope that you caught my point. If not, ask again, and I will try to clarify.
Live long,
The problem lies in notation and in perception, though. I will keep my maths as simple as possible.
Let us look at the pavilion of a round. We agree that we should have good symmetry and a pavilion-angle of around 41°, thus resulting in a pavilion depth of around 43%.
In a princess-cut, the P2-angle, going from the point to the culet, should also be around 41°. But because the depth of a princess is not a factor of the average diameter (like in rounds), but of the smallest diameter, this changes the depth-percentage. Since the facet goes from the corner to the culet, the depth is about 43% of the longest diameter (from point to point). In gemology however, we use the smallest diameter as a reference, and suddenly, the same pavilion-angle causes a depth of slightly over 60%. So, same rules, same angle, but different notation.
In the same way, I like a crown angle in a princess-cut, which is around 34°. Reminds me a lot of what I like in a round.
They have become different animals, however, because the notation of the proportions is different. If you have a princess with a total depth of 63%, this would be under 55%, if we would calculate it in the same way as in a round. Are you sure that you would want to have a round with only 53%-depth?
Sorry, I am beginning to ramble. I hope that you caught my point. If not, ask again, and I will try to clarify.
Live long,
:)
Brilliant_Rock
- Joined
- Jul 25, 2006
- Messages
- 1,864
You may have missed this last time I posted it on your thread due to the fast moving nature of the thread..
http://diamonds.pricescope.com/fnc1.asp
http://diamonds.pricescope.com/fnc1.asp
If you''re shopping in the DD be very careful - especially with that much money!
There are lot of malls in the DD that rip-off people - especially the ones which are accessible to the general public. Unless you have an appointment with a trustworthy diamond dealer in a secure buliding somewhere. Or Tiffanys / Cartier
I still think you should have a look at the AGS ACA / Ideal-000 Princesses on whiteflash. You really can''t judge a Princess by the maths and unless you''ve seen an AGS000 before, it''s easy to be taken for a ride.
There are lot of malls in the DD that rip-off people - especially the ones which are accessible to the general public. Unless you have an appointment with a trustworthy diamond dealer in a secure buliding somewhere. Or Tiffanys / Cartier
I still think you should have a look at the AGS ACA / Ideal-000 Princesses on whiteflash. You really can''t judge a Princess by the maths and unless you''ve seen an AGS000 before, it''s easy to be taken for a ride.
- Joined
- Sep 2, 2002
- Messages
- 2,859
belle
Super_Ideal_Rock
- Joined
- Nov 19, 2004
- Messages
- 10,285
thanks for the bump paul, i had not seen your previous reply. you make excellent points of course, unfortunately i think the op may need to attend your diamond basics course before digesting this hearty chunk of meat. after all, not everyone understands the impact of a round with only 53% depth. much less how it relates to that of a princess.


- Joined
- Aug 15, 2000
- Messages
- 19,089
I think this is intersting Paul - could you give me the other two angles and tables size - because according to the AGS charts there is not many good matches around that zone for at least the 65% table size.Date: 1/17/2007 11:47:10 AM
Author: Paul-Antwerp
My reply might surprise you, but I think that princess-cuts follow the same rules as rounds. After all, it is the same material, diamond, and it is the same light entering from the environment, isn''t it?
The problem lies in notation and in perception, though. I will keep my maths as simple as possible.
Let us look at the pavilion of a round. We agree that we should have good symmetry and a pavilion-angle of around 41°, thus resulting in a pavilion depth of around 43%.
In a princess-cut, the P2-angle, going from the point to the culet, should also be around 41°. But because the depth of a princess is not a factor of the average diameter (like in rounds), but of the smallest diameter, this changes the depth-percentage. Since the facet goes from the corner to the culet, the depth is about 43% of the longest diameter (from point to point). In gemology however, we use the smallest diameter as a reference, and suddenly, the same pavilion-angle causes a depth of slightly over 60%. So, same rules, same angle, but different notation.
In the same way, I like a crown angle in a princess-cut, which is around 34°. Reminds me a lot of what I like in a round.
They have become different animals, however, because the notation of the proportions is different. If you have a princess with a total depth of 63%, this would be under 55%, if we would calculate it in the same way as in a round. Are you sure that you would want to have a round with only 53%-depth?
Sorry, I am beginning to ramble. I hope that you caught my point. If not, ask again, and I will try to clarify.
Live long,
But i agree with your premise that when the angles are measured from the longest corners on the pavilion the results are the same.
However this is not true for french cornered stones where the same comparison could hold as it is the only facet on the princess crown that could have a similarity to a crown angle on a round. This facet would surely be at a much lower angle on a nice princess (if the french corner is used).
- Joined
- Sep 2, 2002
- Messages
- 2,859
Hey Garry,
How about 60 table, pavilion 59-41 and crown 34-28?
You are right and wrong with your comment on the crown and french-corner. This corner-facet is indeed technically comparable to the main crown-facet. But their surface is in comparison very small.
Stars for instance, in a round, have an angle of around 23°. So, maybe an second crown-angle of 28° in a princess offer more possibility of fire, provided the other angles are OK?
Anyway, in all comparisons, the importance of the pavilion is much higher than that of the crown.
Live long,
How about 60 table, pavilion 59-41 and crown 34-28?
You are right and wrong with your comment on the crown and french-corner. This corner-facet is indeed technically comparable to the main crown-facet. But their surface is in comparison very small.
Stars for instance, in a round, have an angle of around 23°. So, maybe an second crown-angle of 28° in a princess offer more possibility of fire, provided the other angles are OK?
Anyway, in all comparisons, the importance of the pavilion is much higher than that of the crown.
Live long,
- Joined
- Aug 15, 2000
- Messages
- 19,089
- Joined
- Aug 15, 2000
- Messages
- 19,089
I agree the pvilion is always most critical.Date: 1/22/2007 11:23:21 AM
Author: Paul-Antwerp
Hey Garry,
How about 60 table, pavilion 59-41 and crown 34-28?
You are right and wrong with your comment on the crown and french-corner. This corner-facet is indeed technically comparable to the main crown-facet. But their surface is in comparison very small.
Stars for instance, in a round, have an angle of around 23°. So, maybe an second crown-angle of 28° in a princess offer more possibility of fire, provided the other angles are OK?
Anyway, in all comparisons, the importance of the pavilion is much higher than that of the crown.
Live long,
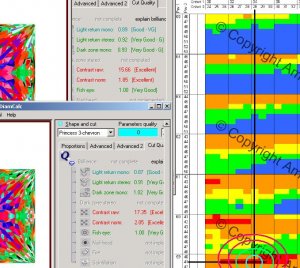
This set does work for both 2 and 3 chevrons Paul - but it is a small target on the AGS chart
- Joined
- Sep 2, 2002
- Messages
- 2,859
- Joined
- Sep 2, 2002
- Messages
- 2,859
Bunnifer
Shiny_Rock
- Joined
- Sep 26, 2006
- Messages
- 227
- Joined
- Jul 25, 2005
- Messages
- 13,375
- Joined
- Aug 15, 2000
- Messages
- 19,089
A round diamond needs only table, crown and pavilion angle to tell if it is well proportioned - there are only minor influences from other facets that have about 1 in 100 chances of being bad.Date: 1/23/2007 4:25:53 PM
Author: Bunnifer
So, most of this discussion is over my head (*whoooosh*) but could either Garry or Paul deduce a desired pavillion angle/crown angle combo? Or is this kind of info useless?
Sorry...it''s hard to wrap your mind around the above concepts.
Most fancy shapes have 2 or 3 each of crown and pavilion angles. $ facet asschers have 4 of each.
Then you have non square stones and everything changes again.
That is why proportions that are given here often by people wanting advice are next to useless.
Princess have 2 each crown and pavilion - and that is what Paul is giving me.
Here is the full aGS princess chart for 60% table sizes (only) - look at the blown up version on my earlier post and you can see the complex axes with 2 lots of data to select from on each axis.
Now lok at this one and you can see AGS tyhink there are lots of proportions sets with red good zones - and huge ranges of bad zones

- Joined
- Aug 15, 2000
- Messages
- 19,089
- Joined
- Sep 2, 2002
- Messages
- 2,859
Because a few posters have indicated that this thread is way too technical for them, let me try to rephrase the most important part.
A round brilliant is a rather simple geometrical shape, and a big part of the cut-information can be deducted from a minimal number of proportions, being table size, average main pavilion angle, average main crown angle, girdle thickness and total depth. Even if one only has total depth and table size, this already gives us a minimum of info, not sufficient to judge, but sometimes sufficient to reject.
A princess-cut is more complicated in shape, and works with two main pavilion angles and two main crown angles. So, if we are looking for the full info, we definitely need to have all these angles.
The original question however was whether one could also deduct info from the basic info (table, depth, girdle), similarly like in rounds, and if this works according to the same rules. In other words, if one is looking for a table of around 60% in rounds, and a depth not higher than 61.5%, do the same rules and figures apply to a princess-cut?
The difference between ''rules'' and ''figures'' is the origin of a complicated matter.
If we talk about rules, we are talking about the interaction of light and diamond, and the basic rules are the same for a round and a princess. So, if we look at the most important proportion, the pavilion angle, I am not surprised to see that a P2-angle around 41° yields a very good result in a princess-cut, just as it is a very good target in a round.
However, when talking about figures, the whole thing becomes very complicated. Depth-percentages in a round are percentages of the average diameter of the stone. In a princess-cut, depth-percentages are percentages of the smallest diameter. Because the system of notation is different, the figures cannot be compared.
In this way, with the same pavilion-angle, one gets totally different depth-percentages. A pavilion angle around 41° will give a pavilion depth around 43% in a round. In a princess, the same angle will give a pavilion depth around 60%. Same angle, different figures.
Hope this clears up the matter somewhat,
A round brilliant is a rather simple geometrical shape, and a big part of the cut-information can be deducted from a minimal number of proportions, being table size, average main pavilion angle, average main crown angle, girdle thickness and total depth. Even if one only has total depth and table size, this already gives us a minimum of info, not sufficient to judge, but sometimes sufficient to reject.
A princess-cut is more complicated in shape, and works with two main pavilion angles and two main crown angles. So, if we are looking for the full info, we definitely need to have all these angles.
The original question however was whether one could also deduct info from the basic info (table, depth, girdle), similarly like in rounds, and if this works according to the same rules. In other words, if one is looking for a table of around 60% in rounds, and a depth not higher than 61.5%, do the same rules and figures apply to a princess-cut?
The difference between ''rules'' and ''figures'' is the origin of a complicated matter.
If we talk about rules, we are talking about the interaction of light and diamond, and the basic rules are the same for a round and a princess. So, if we look at the most important proportion, the pavilion angle, I am not surprised to see that a P2-angle around 41° yields a very good result in a princess-cut, just as it is a very good target in a round.
However, when talking about figures, the whole thing becomes very complicated. Depth-percentages in a round are percentages of the average diameter of the stone. In a princess-cut, depth-percentages are percentages of the smallest diameter. Because the system of notation is different, the figures cannot be compared.
In this way, with the same pavilion-angle, one gets totally different depth-percentages. A pavilion angle around 41° will give a pavilion depth around 43% in a round. In a princess, the same angle will give a pavilion depth around 60%. Same angle, different figures.
Hope this clears up the matter somewhat,
- Status
- Not open for further replies. Please create a new topic or request for this thread to be opened.
Share:
The Ultimate Guide to Men’s Wedding Bands: Metals, Fit & Finish
The Ultimate Guide to Men’s Wedding Bands: Metals, Fit & Finish - 06/27
Chipped Diamonds: Causes, Risks, and What You Should Do About It
Chipped Diamonds: Causes, Risks, and What You Should Do About It - 06/27









300x240.png)