Find your diamond
Find your jewelry
shape
carat
color
clarity

Statistical Analysis of Diamond Pricing

J

jyliu86

Rough_Rock
Joined
Sep 2, 2014
Messages
15
Foreword: So, I fell in love with a girl. I want to marry her. To do this, I need to get a diamond ring. And none of that is really relevant to this discussion :) This is going to be long. It's going to have math. You'll probably get pretty bored reading this. But I hope that somewhere, someone will find my research useful. Enjoy.

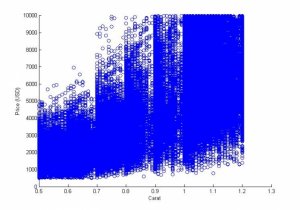
I'd like to answer a seemingly simple question, "How much should I expect to pay for a diamond?" Unfortunately I'm a jaded human being and I don't think I'll ever get an honest answer if I just ask somebody. So, no personal anecdotes, no talking to sales people, let's just look at solid numbers. Thankfully, we have the Internet. This is going to be a very focused analysis of round brilliant loose stones only. I'm not looking at settings. And I'm not looking at any other fancy cuts. I'm lucky in that I know what my girlfriend wants.

So here's what I've done so far. I went to http://www.diamondse.info This is a large database of diamonds. These are real diamonds that I can buy with a few clicks. I assume it's large enough to be a statistically significant sample of the full population of stones on the market. And more importantly to me, relatively easy to data mine. I wrote a script to crawl this website and extract 306560 individual stones with prices. I limited my search for round brilliant stones priced $0-$10,000 USD. My data set was taken 8/25/2014.

My expectation is that price can be determined as a function as:

PRICE = F(CARAT, CUT, COLOR, CLARITY)
specifically:
Price = C0 + C1*Carart + C2*Cut + C3*Color + C4*Clarity
where C0, C1, C2, C3, and C4 are constants.

My first pass is going assume a linear relationship and use multiple linear regression. Multiple linear regression requires integer input, so I'm going to map color, cut and clarity codes to numbers. Because I want my coefficients to have similar weights, and I'm going to pretend that a "typical" carat is 1, I'm going to scale the other factors from 0-1.

Cut Mapping:
Hearts & Arrows = 1
Ideal = 5/6
Very Good = 4/6
Good = 3/6
Fair = 2/6
Poor = 1/6

Color Mapping
D=1
E=0.9
F=0.8
G=0.7
H=0.6
I=0.5
J=0.4
K=0.3
L=0.2
M=0.1

Clarity
F=1
IF=10/11
VVS1=9/11
VVS2=8/11
VS1=7/11
VS2=6/11
SI1=5/11
SI2=4/11
I1=3/11
I2=2/11
I3=1/11

I put all that into Excel and run a Regression Analysis and:

PRICE = -9172.929 + 9073.0*Carat + 1538.85*Cut + 3173.84219*Color + 4315.93*Clarity
With R^2 = 0.80164

Looks like a decent model at first glance. But there are plenty of problems with this model that I'll get to addressing.
 
Good first steps... looking forward to seeing more. As you are likely already aware (and will likely address), the rarity factors should be much more heavily weighted as carat weight increases.
 
First the lab that did the grading has the highest impact on the price for any given grades.
2 stones one graded by egl international one by GIA both have the same grade on paper but can sell for over 50% difference in price or more because of the lax grading and bad reputation of egl.

Second there are a lot of things not on the grading report that effect the price even for diamonds graded by the same lab with the same grades.
 
Nice start. A few comments.

The scales are not linear. The increase in price for H->G is not the same as for J->I.

It's also not the same across clarities. That is to say, the price premium for G vs. the premium for the I isn't the same with VVS as it is for I1's.

The increase in price per carat is decidedly not linear and there are some very distinct jumps. A 2.01 will be bunches more than an otherwise similar 1.95 while a 1.90 and a 1.95 will be about the same. A with the above, the amount of this will vary with the clarity and color grades.
 
So I wanted to plot the error of my model, vs. real pricing. Unfortunately, Excel blows up at 32000 data points and I have significantly more than that. So I moved all my stuff into MATLAB. Unfortunately I don't have MATLAB's statistics toolbox so I have to write my own functions. In doing so, I found out that during the matrix multiplication necessary blows up my computer's memory. So, I divided my data set into chunks of ~5000 elements each. I do this by

1) Sorting by price low to high.
2) Set 1 corresponds to element 1, element 61, element 121... until i reach the end.
2) Set 2 corresponds to element 2, element 62, element 122 and I do this until I have ~60 sets.

For each set I run a multiple regression. Then I average my coefficients. So how'd I do:

MATLAB version:
Price = -9180.2 + 9077*Carat + 1538.9*Cut + 3174.9*Color + 4322.8*Clarity
EXCEL version:
PRICE = -9172.929 + 9073.0*Carat + 1538.85*Cut + 3173.84219*Color + 4315.93*Clarity
With R^2 = 0.80164

These look close enough that I can work with my MATLAB version. So I plot error vs. carat. I'll post the actual figure later, but to summarize... not good.

I've got a minimum error of +/-$1500. Error also trends upward, which gets to my first issue. As many readers have already pointed out while I was writing this, I don't believe that any of the parameters of diamond pricing scale linearly. I fully expect that price with respect to carat is not linear. Same with color, clarity and cut. I'll need to adjust my model to account for this.

Also, after doing some shopping and physically comparing diamonds, different laboratories use the same nomenclature, but end up grading stones differently. So, to make things easier for my initial model, I will consider GIA graded diamonds ONLY. I'll post that model when I get it up.
 
Your model doesn't capture one of the key aspects of finding a diamond: cut

It is not as cut and dry as the categories you have defined, with even 'Ideal' stones not meeting the same standard.

You have to compare apples to apples here.

Unfortunately, you'll find regression analysis largely invalid here, as the variability of the data points (and whether we have access to the totality of that data) is too great.

Not all 'I-colored' stones are the same. Not all 'Ideal' stones are the same. Not all 'SI1' stones are the same. EVEN FROM THE SAME LAB! This only makes the possibility of well-defined parameters more difficult.

I'd love to be able to set up a function to effectively model this, but I feel it's largely a wild goose chase.


Disclosure: I wrote my Master's thesis on regression analysis


EDIT: You had posted since my last message. Reducing the data set to all GIA stones will still not be able to be modeled effectively. Since there is a range of 'GIA XXX' stones, some better than others, but all receiving the same grade from GIA, it is impossible to remove this confounding factor. Yet another factor is clarity: SI1's that are eye-clean and those that are not command different prices. There are also 'high H-colored' stones and 'low H-colored' stones, both of which command different pricing to the end user.
 
I'm ok with this being a wild goose chase. First pass, with 0 refinement, I have error bars of +/- $4000 at 1.0 carats. It's a laughably bad model, but I can do better.

Even if my error bars are laughably bad, I'm in a better place than I started. Everything is impossible before it's done. Worst case, I've wasted a few hours of my life doing math.

I have no doubt in my mind, that my model will not be perfect. But If I can get to a point where I can say an GIA graded SI1 J 1.1 carat stone is $6000 +/- $500 with 95% confidence interval, I'll call that a success.

There's a pretty good point with regard to cut being a nebulous term. I'm just being lazy about it. If I'm finding that GIA cut grades are too "loose" I'll start including table, depth, and angles into the model.
 
In response to RockyRacoon, I filtered my data to only look at GIA, 1.0 carart, Ideal Cut, I color, SI1 diamonds.

Samples: 303 diamonds
Range: 4241 - 7123 (7123 looks like outlier)
Average: 5320.521
STDDEV: 384.92
Median: 5300

Ran a quick histogram, data looks kind of normal. This is a surprisingly large spread. Kudos RockyRacoon. I'll see if I can find other criteria to shrink the spread down. Vendor is the most obvious I can think of.
 
What's the point?

Here on PS we already know how and where to get high quality for low price.

And again you have not even brought up cut quality, the most important factor that determines diamond beauty.
 
kenny|1411517531|3756038 said:
What's the point?

Here on PS we already know how and where to get high quality for low price.

And again you have not even brought up cut quality, the most important factor that determines diamond beauty.
Click to expand...
Idunno1.gif
 
I did include cut, in the admittedly laziest way possible. I used the diamondse.info's cut grading, which corresponds to GIA cut gradings when I limit my data set, plus one additional Hearts and Arrows grade they use to sell their "special" cut stones.

Sure, I can include a table and depth ratios. Ideally I'd include pavilion and crown angles, which are unfortunately, not always readily available for bulk data mining. So I took the easy route, and the one most consumers are going to see, cut grade. There is plenty of reason to argue that cut grades simply aren't a good way to pick a diamond. I am in no way trying to claim that I'm modelling a good way to purchase a stone, or any stone analyzed with my model is a good or bad deal.

I'm only trying to figure out how vendors will price their diamonds. I'm sure some of them have nice pretty tables with rows and columns listing all the parameters or at least insurance appraisers do. I've certainly never seen one. I'd love to see one if any of those are publicly available.

This is ultimately, my research to figure out how much I'm going to pay when I get an engagement ring. If someone else finds my research useful, great! If not, I'll be the crazy guy posting in this thread.
 
Thank you for your input. That's a lovely stone.

I probably would try another vendor like:
http://www.uniondiamond.com/Round-Brilliant-Shape-Select-Ideal-Cut-GIA-Certified-110-Carat-J-Color-VS2-Clarity_AE0756759&ptc%3DDSE
A quick run through the HCA grades it as 1.0. The angles and %'s look good to me, but I don't have tons of experience looking at live stones. Still, I'd image it would be "good enough".

My girlfriend is actually quite sensitive to color. The setting she's interested has side stones colored G, so the J's don't show as nicely compared to them. We went into the jewelry store and using a J colored diamond as the center stone was unacceptable to her. Of course, the sales rep could have shown us a stone that was subpar in other parameters. Given her small fingers scaling down to 0.9 carat is acceptable. She has a size 4 finger, so the center stone will still have cover ~40% of her finger width.

----

Even if my variance is going to be high, I'm going to move my goalposts backwards and say it's "good enough" for now. Even constraining everything, 3 sigma is +/- ~$1200. I'll figure out how to deal with that later. I'd like to deal with the non-linearity first.

So easy one, carat. I've plotted prices v. carat. See the attachment.


The first thing that's immediately obvious is I cut data set too low. I set my max price on the crawl to $10,000, which is well above anything I planned to spend, but too low for this data set. I'll kick it up higher and run my crawler overnight. It looks like there's a pretty strong non-linear relationship, but it's hidden in the mess.

I'm going to bin the data by carat, and hope that large numbers and averages give us something better to look at.

The spread is ok. I'm not doing any binning by cut, clarity or color, which is going to cause huge spreads. But averaging should help neutralize that. After I get the appropriate linear transform, I'll rerun the full multiple regression and see if the results are better.

price_v_carat_all.jpg
 
jyliu86|1411514785|3756009 said:
I have no doubt in my mind, that my model will not be perfect. But If I can get to a point where I can say an GIA graded SI1 J 1.1 carat stone is $6000 +/- $500 with 95% confidence interval, I'll call that a success.
Click to expand...

Agreed.
 
Hey, turns out averaging works! Here's a plot of average price vs. carat. Relationship looks sorta exponential, but because I cut off my price too early my data cuts off before I can definitely say what kind of model to use. I included a linear trendline, which is clearly wrong, for comparison.


I'm going to wait for my new data set before I continue.

For those interested in the math, I binned in intervals of 0.01 carat, which is as fine as my data set goes.

carat_v_avgprice.png
 
Dancing Fire|1411521188|3756057 said:
jyliu86|1411520612|3756053 said:
This is ultimately, my research to figure out how much I'm going to pay when I get an engagement ring. If someone else finds my research useful, great! If not, I'll be the crazy guy posting in this thread.
Click to expand...
Here!.. done your home work in 5 secs... :praise:
http://www.briangavindiamonds.com/diamonds/diamond-details/1.092-j-vs2-round-diamond-ags-104067108129#!prettyPhoto[gallery2]/3/
Click to expand...

Now that is funny DF. :lol:

OP, I'm in awe of your effort here, math is not my strong suit--kudos to you.
 
Hmm (any other stats nerds out there?) I wonder what the lme and lme4 packages in R would make of this data set?

You assume that modeling all the variables would yield the best model, but It might turn out that 1 or 2 key variables are the main determinants and that the other variables are actually not that important. I wish I had more time to explore this.

(Great find of a nice stone DF! If I was in a buying mood... :naughty: )
 
this is quite interesting. :read:

I too wonder if the simplifications that OP is using to make the regression analysis more manageable are the right ones, in a diamond context. As others have pointed out, the regression treats the step between an I1 and SI2 the same as VVS2 to VVS1. I understand why, from a stats perspective, that you have made the choices you have made... but if the purpose of the analysis is to anticipate the way a vendor would price his stones, shouldn't we choose data inputs that mirror what we actually do know about pricing?

My regression abilities are admittedly limited, but would there be a place for some dummy variables that might correct for some of this - perhaps something that accounts for being at/over/near a "magic" weight, for example?

Hoping other nerds chime in too :)
 
tuckie|1411585194|3756472 said:
this is quite interesting. :read:

I too wonder if the simplifications that OP is using to make the regression analysis more manageable are the right ones, in a diamond context. As others have pointed out, the regression treats the step between an I1 and SI2 the same as VVS2 to VVS1. I understand why, from a stats perspective, that you have made the choices you have made... but if the purpose of the analysis is to anticipate the way a vendor would price his stones, shouldn't we choose data inputs that mirror what we actually do know about pricing?

My regression abilities are admittedly limited, but would there be a place for some dummy variables that might correct for some of this - perhaps something that accounts for being at/over/near a "magic" weight, for example?

Hoping other nerds chime in too :)
Click to expand...

Even if you dummied this up, it wouldn't be able to take into account the complexity of the data. Judging by grades (using certificates) and using more fluid/dynamic methods (used by the seller to actually price the good), creates a disparity that can't be bridged.

Data would need to be more discrete to really make this analysis explanatory.
 
Are you buying a diamond for the woman you love or a ham sandwich diamonds demand more attention to their beauty in cut in personality then putting numbers into an equation geeze.....poor girl
 
jyliu86--you haven't told us your end game in all of this: is it just a fun exercise? or are you trying to develop a model to find a best value, beautiful diamond (which, btw, is near hearts & arrows, well proportioned ideal cut, H-I SI1-2, VG symmetry and polish, just below each non-linear price jump, e.g. 0.85-.99, 1.15-1.24, faint fluoro, from a low-overheard retailer like Blue Nile or James Allen)?
 
For the sake of discussion, I'm doing this for fun.

@heididdl Every time someone has recommended a diamond for me, it's about 1.2x-1.5x more than when I redo the search for a diamond with the same specifications, including table, depth, crown and pavilion angles myself. I will happily pay a 20%-50% premium on a $5 ham sandwich for convenience. I will not pay a 20%-50% premium on $5000. My girlfriend happily agrees with my outlook on life. That's one of many reasons I'd like to marry her.
 
Hi,

OP, I've enjoyed your exercise. Personally, I think you are an interesting guy. Please continue and Rocky can check you.
I'm sure you will find a lovely diamond, Rocky can help with that as well.


Annette
 
jyliu86|1411655413|3756823 said:
For the sake of discussion, I'm doing this for fun.

@heididdl Every time someone has recommended a diamond for me, it's about 1.2x-1.5x more than when I redo the search for a diamond with the same specifications, including table, depth, crown and pavilion angles myself. I will happily pay a 20%-50% premium on a $5 ham sandwich for convenience. I will not pay a 20%-50% premium on $5000. My girlfriend happily agrees with my outlook on life. That's one of many reasons I'd like to marry her.
Click to expand...


That's terrific.
 
jyliu86|1411655413|3756823 said:
For the sake of discussion, I'm doing this for fun.

@heididdl Every time someone has recommended a diamond for me, it's about 1.2x-1.5x more than when I redo the search for a diamond with the same specifications, including table, depth, crown and pavilion angles myself. I will happily pay a 20%-50% premium on a $5 ham sandwich for convenience. I will not pay a 20%-50% premium on $5000. My girlfriend happily agrees with my outlook on life. That's one of many reasons I'd like to marry her.
Click to expand...

Very interesting topic - appreciate you bringing it up. I hadn't thought about pricing using this framework before, so it was a good mental exercise for me, as well.

No need to pay more than a fair price for a stone. It's important to remember that the same numbers do not equal the same stone, so it is often difficult to compare apples-to-apples, based on paper alone.

Being logical when it comes to money eliminates a lot of relationship issues, so it looks like you made a good choice on that front!

Let us know your budget and some general specs, if you'd like some suggestions.
 
I'm wondering how tight you could get a model even within a subset of these C's: eg. G-H (maybe even I?), VS1-2, 1.0-1.2 ?

You would probably get a better grasp of the unexplained variance in what should be a much more linear model. Doing the same for each subset (e.g D-F, IF-VVS2) would then give you a sense of how the weighting of these factors changes, and how much other unaccounted for variables play a role in pricing throughout the spectra of C's.
 
jyliu86|1411655413|3756823 said:
For the sake of discussion, I'm doing this for fun.

@heididdl Every time someone has recommended a diamond for me, it's about 1.2x-1.5x more than when I redo the search for a diamond with the same specifications, including table, depth, crown and pavilion angles myself. I will happily pay a 20%-50% premium on a $5 ham sandwich for convenience. I will not pay a 20%-50% premium on $5000. My girlfriend happily agrees with my outlook on life. That's one of many reasons I'd like to marry her.
Click to expand...
Your approach is entirely logical and it is an interesting and impressive exercise to follow. In the end however diamonds and the diamond market are not themselves entirely logical. Your methodology will put you in the ballpark, but there are much more convenient tools for doing that. Using the search on this site and others, varying the parameters, will give you pretty good indications of the ballpark you will be in for certain size/quality combinations.

If the objective is to better understand the macro market forces, your analysis will lead you in that direction. But when it is time to choose a diamond, it will be of limited help.

Because of the nature of diamonds, it might be a mistake to rule out paying a 20% premium over your statistical "right price". Or for that matter, not to rule out a diamond that is 20% less! Moreover, it's better to think more in terms of value rather than price.

Others have mentioned the differences in labs, differences in characteristics between stones of the same color,clarity and cut grades, There are also other value factors that often contribute to premiums such as the merchants buyback and trade-up policies, gemological services and diagnostics provided, jewelry service benefits and more.

In the final analysis it's necessary to understand more about the combination of individual characteristics of the diamonds themselves in order to make an excellent buy. And the overall value-added proposition associated with a specific purchase including the merchant's reputation and policies.
 
I'm just curious, but what do you do for a living?

(I saw this thread and immediately sent my husband an email, "OMG ARE YOU GETTING ME A DIAMOND?!" as a joke, but he often does stats for fun, so I was entertained by seeing this thread.)
 
You must log in or register to reply here.
GET 3 FREE HCA RESULTS JOIN THE FORUM. ASK FOR HELP
Jewelry Blog
PriceScope-Concierge-Ad
Find prime cuts.
Top