I am quite new to the forums and to diamonds in general. I am quite good at math, however 
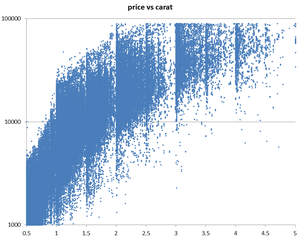
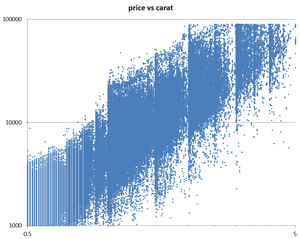
Why is it that everybody seems to claim that "diamond prices rise exponentially with size"? I see this claim repeated everywhere, from beyond4cs to Whiteflash. I am sure that what mean is only that a diamond twice as big will be much more than twice the price, all else being equal. However, that is goes up higher than linear does mean that it goes up exponentially.
If diamond prices raised exponentially with price, then we would have the following:
1ct diamond: Price 5.000$
2ct diamond: Price 20.000$ (4 times more expensive)
3ct diamond: Price 80.000$ (4 times more expensive than 2ct)
4ct diamond: Price 320.000$ (4 times more expensive then 3ct)
5ct diamond: Price 1.280.000$ (4 times more expensive than 4ct).
We know that 4ct and 5ct diamonds are expensive... but not that much. Instead, what I see is a very clear quadratic increase in prices!
1ct diamond: Price 5.000$ (5.000$ per carat)
2ct diamond: Price 20.000$ (10.000$ per carat)
3ct diamond: Price 45.000$ (15.000$ per carat)
4ct diamond: Price 80.000$ (20.000$ per carat)
5ct diamond: Price 125.000$ (25.000$ per carat)
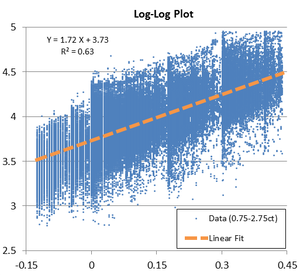
I see that real diamond prices follow this curve almost perfectly. So a diamond two times bigger is 4x more expensive; a diamond three times bigger is 9x more expensive, and so on. A diamond X times bigger has a X times higher price-per-carat.
That works for small changes as well. A diamond that is 1% bigger seems to have an average of (1.01)^2 ~ 1.02 which means it is 2% more expensive.
So I think we can be more precise and start informing buyers that diamond prices rise quadratically with size!
I believe this is a very helpful way of thinking, as it allows a very useful statistic, in my opinion. Instead of talking about price-per-carat, we should start talking about price-per-squared-carat! Just calculate price / (carat * carat).
So if you are paying a higher price-per-squared-carat than you would for a similar stone in another size, you might be paying a premium. At the same time, looking for low price-per-squared-carat can help finding diamonds in a good pricing.
Why is it that everybody seems to claim that "diamond prices rise exponentially with size"? I see this claim repeated everywhere, from beyond4cs to Whiteflash. I am sure that what mean is only that a diamond twice as big will be much more than twice the price, all else being equal. However, that is goes up higher than linear does mean that it goes up exponentially.
If diamond prices raised exponentially with price, then we would have the following:
1ct diamond: Price 5.000$
2ct diamond: Price 20.000$ (4 times more expensive)
3ct diamond: Price 80.000$ (4 times more expensive than 2ct)
4ct diamond: Price 320.000$ (4 times more expensive then 3ct)
5ct diamond: Price 1.280.000$ (4 times more expensive than 4ct).
We know that 4ct and 5ct diamonds are expensive... but not that much. Instead, what I see is a very clear quadratic increase in prices!
1ct diamond: Price 5.000$ (5.000$ per carat)
2ct diamond: Price 20.000$ (10.000$ per carat)
3ct diamond: Price 45.000$ (15.000$ per carat)
4ct diamond: Price 80.000$ (20.000$ per carat)
5ct diamond: Price 125.000$ (25.000$ per carat)
I see that real diamond prices follow this curve almost perfectly. So a diamond two times bigger is 4x more expensive; a diamond three times bigger is 9x more expensive, and so on. A diamond X times bigger has a X times higher price-per-carat.
That works for small changes as well. A diamond that is 1% bigger seems to have an average of (1.01)^2 ~ 1.02 which means it is 2% more expensive.
So I think we can be more precise and start informing buyers that diamond prices rise quadratically with size!
I believe this is a very helpful way of thinking, as it allows a very useful statistic, in my opinion. Instead of talking about price-per-carat, we should start talking about price-per-squared-carat! Just calculate price / (carat * carat).
So if you are paying a higher price-per-squared-carat than you would for a similar stone in another size, you might be paying a premium. At the same time, looking for low price-per-squared-carat can help finding diamonds in a good pricing.
Last edited:







300x240.png)