The matter of depth in a princess-cut

Unfortunately, using well-known and tested procedures for rounds on fancies does not always work, and very often, one could be misled by simply using the rule for rounds on fancies. The depth of a princess-cut is a classic example.In this, both technical as psychological differences are at play.1. The technical difference

A round brilliant is a symmetrical stone with one main pavilion angle and one main crown angle. As such the depth of a stone is a direct result of that pavilion angle, that crown angle in combination with the table size and the thickness of the girdle.

Because of the round brilliant being such a straightforward stone, the rule that depth relates to spread can be applied.

Not so in a princess-cut however. To start, a princess-cut has two main pavilion angles and two main crown angles. On top of that, the table size of a princess varies considerably from 55% up to higher than 80%. Below, you can find an illustration of A.G.S.-Laboratories, which clearly shows the different angles.

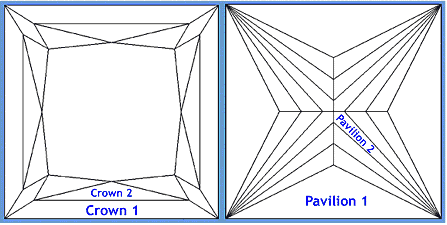
Now, you should pay attention to the pavilion of this stone. The ‘pavilion 2’ goes from the girdle to the culet, and it is therefore this pavilion angle, which sets the pavilion depth.

‘Pavilion 1’ on the other hand can vary considerably in angle, without the pavilion depth being affected. It is precisely in this area that a cutter can hide a lot of weight without the total depth being affected.

2. The psychological difference

When looking at a round brilliant, we are used to seeing total depths around 60%. Psychologically, a total depth of 70% and higher in a princess-cut automatically seems extremely deep.

However, one should consider that both depths are not measured in the same way.

In a round, the total depth is a percentage of the average diameter of the stone. In a princess however, and in any fancy shape, for that matter, the total depth is a percentage of the lowest diameter.

Let us consider a perfectly square princess with a diameter of 6mm. from side to side. With a depth of 4.5 mm., we will calculate a depth percentage of 75%.

However, if we would measure the diameter from point to point, the diameter would be 8.49 mm., and the depth percentage of the highest diameter is only 53.03%.

Now, if we would work with total depth compared to the average diameter of a princess-cut, like we do in rounds, the depth percentage is 62.13%.

You will agree with me that there is a psychological difference between a depth percentage of 75% (traditional measurement) and 62.13% (measured on average diameter).

3. Conclusion

This is a very short, but important article. It shows how even the simplest rules of rounds do not necessarily apply to fancy shapes.

I hope that you have enjoyed this little arithmetic.