Cutting Ovals

Figure 1 shows a 4:3 oval (e.g. 8x6mm) cut using the same indexes (azimuths) as a standard round brilliant and also the same slopes for the main facets (the half-facet slopes must be modified for desired depth and proper meets).

The pavilion, at the upper end, shows a trace of end-facet ‘a’. At the lower end we have modified the adjoining halves ‘ab’ and ‘bc’ to eliminate this useless facet (red lines & data).

The result, as you can see, is not as pretty as we would like. The table does not have the same ratio – it is elongated – and the end facets are squeezed together.

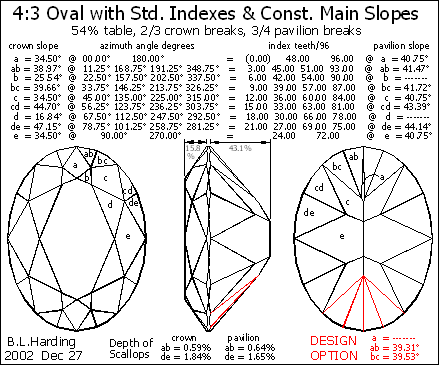
Fig.1 Same indexes & main slopes as round.

Many theorists think that an oval pavilion should come to a point just like a round brilliant. Figure 2 shows the theoretical ideal, which is a round brilliant stretched in one direction but retaining the depths of the original round stone –as though the stone was rubber; Octonus uses this concept in their DiamCalc© software.

This requires cutting similar facets at different azimuths and slopes. Ideally the side mains ‘e’ are the same as the ‘original’ round. The data here are for a 4:3 ratio with ‘best’ slopes for diamond at the side mains. The need to cut at odd azimuths requires a machine with adjustable indexing or special index wheels.

By choosing the same slope for the side mains as for a round brilliant of the same material, there is no ‘bow tie’ reflection of the viewer’s head across the width of the gem; however, the end mains are at a much shallower slope and give poor light return.

Cutters often increase the slope of all facets, increasing the depth of the stone, to reduce this problem but, in so doing, the increased slope of the side facets results in the ‘bow tie’.

Fig.1 Same indexes & main slopes as round.

If you look closely at Fig.1 you can see that the scallops are shallower at the ends; if cut to normal thckness, the scallops at the sides may meet to form a knife-edge.

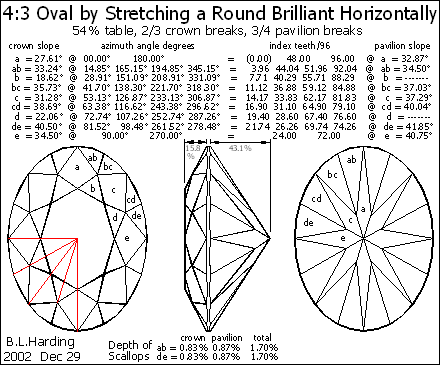
Fig.2 All proportions maintained.

In Fig.2 note the alignment of joins and meets with the red lines, which is indicative of a perfectly-stretched round (compare to Fig.1).

All scallops have the same depth in this design.

Figure 3 shows a cut which is optically better because the slopes of similar facets are the same all the way around the gem; this results in a ridge at the bottom of the pavilion – instead of a point, just as in Fig.2.

In a long oval the end facets ‘a’ of the pavilion may disappear. In this one, which has a 4:3 ratio, these facets are insignificant (as shown at the top) and can be removed by changing the slope or azimuth of halves ‘ab’ and ‘bc’ (as shown in red at the bottom).

In Fig.3 the scallops are uneven but less than in Fig.2.

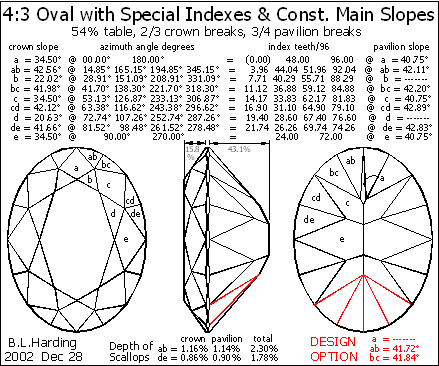
Fig.3 Same main slopes as round but special azimuths.

Fig.3a shows a modification in which four extra facets ‘d’ are cut at the pavilion tip to form a pointed culet; these will be at a lower slope than the mains; all other facets and data are the same as in Fig.3.

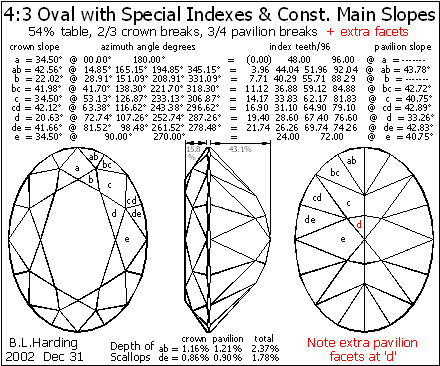
Fig.3a Same as Fig.3 with extra facets at culet.

Figures 3 and 3a are the best designs illustrated here, but both require the special azimuths listed in Fig.1. As stated before, these require equip-ment capable of adjustable azimuths or specially-made index wheels with notches at these azimuths. I made one of these for my own use (Raytech-Shaw faceter), but a factory such as Adri will make them for your diamond-cutting handpieces.

Octonus says that cutters have been unable to make ovals such as they illustrate (Fig.2). The reason is probably that they do not use these special azimuths or vary the slopes properly.

Figure 4 shows the azimuths for a round brilliant that has been stretched by various common ratios (per commercial head findings).

I made only one index wheel, per the 5:4 ratio (the median), and made a fine-looking 4:3 oval with it, so you don’t need them all.

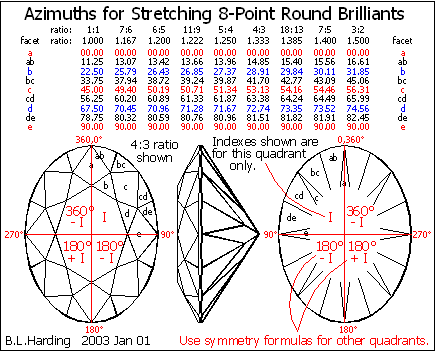
Fig.4 Azimuths for common oval ratios.

B. L. Harding 2006 Feb 04